Thats perfectly normal later well see how the curve is built. 562 and other interrogation problems such as singularities and inflection points.

13 Bezier Representation Of A Functional Curve Download Scientific Diagram
B-Spline is a basis function that contains a set of control points.
. No curves at all. You can play around with 34 and 5 point Beziers or the Bernstein. A domain is convex if for any two points and in the.
A Bezier curve section can be filled by any number of control points. A Quadratic Bezier Curve b Cubic Bezier Curve Figure 5. The first and last points mark the beginning and end of the path while the intermediate points define the paths curvature.
One of the fundamental problems when working with curves is curve fitting or determining the Bézier thats closest to some source curve. First we observe that finding intersections in this case means that given a circle defined by a center point c xy and a radius r we want to find all points on the Bezier curve for which the distance to the circles center point is equal to the circle radius which by definition means those points lie on the circle and so count as. - created by using mathematical to reprint the curve.
The first derivative of a Bézier curve which is called hodograph is another Bézier curve whose degree is lower than the original curve by one and has control points Hodographs are useful in the study of intersection see Sect. In your spare time I suggest you read it in its entirety. Four points P 0 P 1 P 2 and P 3 in the plane or in three-dimensional space define a cubic Bézier curve.
The control points dictate the shape of the curve. Given n1 points P 0 P 1 P 2. A Bezier curve with both terminals at 3 11 and three control points.
And P n in space the control points the Bézier curve defined by these control points is. A quadratic Bezier curve left and a cubic Bezier curve right. Notice how the shape of the Bezier curve dark mimics the shape of the control polygon light.
Bezier Curve Properties- Few important properties of a bezier curve are- Property-01. To save you time heres a link to the Bezier curves section. It is commonly implemented in computer graphics such as vector imaging which uses quadratic and cubic Bézier curves.
Investigating Bezier curves adds a new dimension to the problem of curve sketching. The endpoints bracket the space curve. As such they are a fundamental tool in vector graphics.
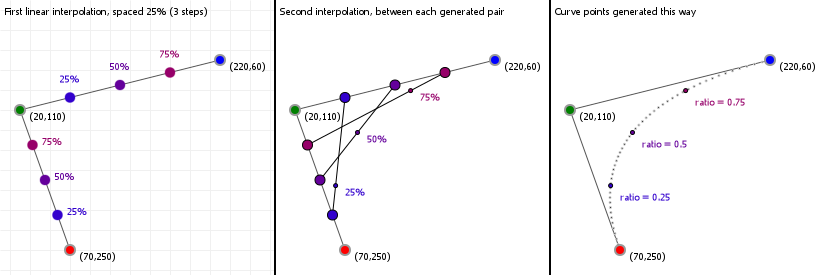
Let Bt be a Bezier curve of degree n and let Q m t denote the control polygon that represents Bt as a Bezier curve of degree m nThen lim m Q m t BtThat is the control polygons generated by degree elevation converge uniformly to the original Bezier curve. Point Q0 varies from P0 to P1 and describes a linear Bézier curve. Where the coefficients are defined as follows.
- Bezier curve generation for higher dimensions is known as Bezier surfaces. Point Q1 varies from P1 to P2 and describes a linear Bézier curve. What are their features.
The B-Spline curves are specified by Bernstein basis function that has limited flexibility. Therefore the point that corresponds to u on the Bézier curve is the weighted average of all control points where the weights are the coefficients B ni u. The label on each edge must be normalized by dividing by b a.
B t 1-t 3 P0 3 1-t 2 tP1 3 1-tt 2 P2 t 3 P3. The values of x and y are determined independently according to a third parameter dubbed t. Intermediate nodes of the de Casteljau.
Where P0 and P3 are the start and end points and P1 and P2 are the first and second control points. Senay Baydas Bulent Karakas 2019 Defining a curve as a Bezier curve Journal of Taibah University for Science 131 522-528 DOI. - Bezier curve is parametric curve.
A Bézier pronounced bez-E-A curve is a line or path used to create vector graphics. A Bézier curve is a curved line or path that is the result of a mathematical equation called a parametric function. There may be 2 3 4 or more.
- Low order Bezier curves are patched together while using more complex. A Bézier curve is a parametric curve frequently used with computer graphics. Graphics software programs often come with tools that generate and manipulate Bézier curves.
They are visually intuitive to use in a software GUI because dragging a control point updates the curves in real time. The shape of a Bezier curve can be altered by moving the handles. Noun a mathematical curve that is often used in computer graphics to model fluid shapes and in animation.
For instance two points curve. This bezier curve is defined by a set of control points b 0 b 1 b 2 and b 3. Least square method is used to approximate the Bezier curve.
If you look closely at these curves you can immediately notice. Points are not always on curve. A cubic Bezier curve is a vector function in terms of the scalar parameter t with end points P 0 and P 1 and control points C 0 and C 1 as defined in Eq1.
- Controlling motion in animations is implemented by Bezier curves. A bezier curve is defined by control points. Points b 1 and b 2 determine the shape of the curve.
To best explain Bezier curves well start with a simple example. You want to make sure that the finished brochure will meet the clients needs. The curve starts at P 0 going toward P 1 and arrives at P 3 coming from the direction of P 2In general it will not pass through P 1 or P 2.
Points b 0 and b 3 are ends of the curve. Applications include simplifying existing paths efficiently. These curves are specified with boundary conditions with a characterizing matrix or with blending function.
Which 3 communication techniques will help you do that. This is the general formula for a cubic Bézier. Fitting cubic Bézier curves.
The curve is defined by four points. Proof By construction Q m t is a piecewise linear curve over the interval 01 and Q m km is. Point Bt varies from Q0 to Q1 and describes a quadratic Bézier curve.
To cite this article. It is a mathematical description of a smooth curve that is defined by representative points. Perhaps this metaphor best describes the sense of a Bezier curve if not its mathematics.
- Bezier curves are used to model smooth curves in Vector Graphics. First theres an excellent site that describes some of the mathematics that we should all know. Which 2 of the following best describe a Bezier curve.
Bezier curve is always contained within a polygon called as convex hull of its control. These points are only there to provide directional informationThe distance between P 0 and P 1 determines how long the curve moves into. Construction of Bézier Curves.
It consists of two or more control points which define the size and shape of the line. A Bezier curve is a mathematically defined curve used in two-dimensional graphic applications. For quadratic Bézier curves one can construct intermediate points Q0 and Q1 such that as t varies from 0 to 1.
The initial position and the terminating position which are called anchors and two separate middle points which are called handles. What describes images that are no longer protected under copyright law. Cubic Béziers are by far the most common curve representation used both for design and rendering.



0 Comments